Spreadsheet Models for Managers
Getting Access to Spreadsheet Models for Managers
If 
you use Excel to model businesses, business processes, or
business transactions, this course will change your life. You’ll learn how to create tools for yourself that will amaze
even you. Unrestricted use of this material is available in two ways.
- As a stand-alone Web site
- It resides on your computer, and you can use it anywhere. No need for Internet access.
- At this Web site
- If you have access to the Internet whenever you want to view this material, you can purchase on-line access. Unlimited usage. I’m constantly making improvements and you’ll get them as soon as they’re available.
To Order On Line
| Order "Spreadsheet Models for Managers, on-line edition, one month" by credit card, for USD 69.95 each, using our secure server, and receive download instructions by return email. |
| Order "Spreadsheet Models for Managers, on-line edition, three months" by credit card, for USD 199.00 each, using our secure server, and receive download instructions by return email. |
| Order "Spreadsheet Models for Managers, downloadable hyperbook edition" by credit card, for USD 199.00 each, using our secure server, and receive download instructions by return email. |
To Order by Mail
Make your check payable to Chaco Canyon Consulting, for the amount indicated:
|
And send it to: Chaco Canyon Consulting 700 Huron Avenue, Suite 19C Cambridge, MA 02138 |
To use the course software you’ll need some other applications, which you very probably already have. By placing your order, you’re confirming that you have the software you need, as described on this site.
Spreadsheet Models for Managers
Demonstrations for Session 2
Analysis and Synthesis
This session emphasizes the use of arrays and matrix multiplication to decompose problems into parts, and then to recombine the parts to form the results we seek. We have one demonstration (2007+) for this session: Using Array Computations in Excel.
Using Array Computations in Excel (2007+)
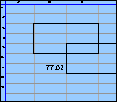
[Sheet: Furniture]
In this example, we’re given an array of furniture prices (FurniturePrices), an array of furniture requirements for a range of job categories (FurnitureAnalysis), and a breakdown of the total headcount by employee category (EmployeeAnalysis). We’re asked to compute the breakdown of furniture required, by type.
All we must do to find the array of furniture we need (FurnitureAllocation) is to multiply the FurnitureAnalysis by the EmployeeAnalysis, as an array product. This has the effect of multiplying each row of FurnitureAnalysis by the number of employees of that type.
To find the cost of this amount of furniture, we use either of two approaches, which yield the same result. In the first approach, we multiply FurnitureAllocation by FurniturePrices, using array multiplication. Then we sum up the cells of this range, and the result is in C35.
In the second approach, we use matrix multiplication:
Of course, whenever we use MMULT or TRANSPOSE, we must enter the formula as an array formula.
Here we transpose EmployeeAnalysis, because its dimensions are (Category x 1) and those of FurnitureAnalysis are (Category x ItemType). The matrix product of the result is therefore (1 x ItemType). When we matrix multiply that by FurniturePrices, which is (ItemType x 1), the result is (1 x 1), which is just a number, and the total we seek.
In the next part, we’re given the hiring streams for all categories of employees, in a range called HiringAnalysis, and we’re asked to compute the cash stream that pays for the furniture of new hires. We can do this in a single formula using matrix multiplication:
This forms the product of three matrices. You might be wondering why we didn’t write this as
Mathematically, this would be correct, but Excel’s mmult accepts only two arguments. That’s why MMMult is provided in the Special Tools for This Course. MMMult can accept arbitrarily many arguments.
Whether you use MMMult or MMult, the units of this product, using dimensional analysis, are $/item * items/headcount * headcount = $. The matrix shapes are
The result thus has units of $ and is a single row six months wide.
Next, we seek the procurement schedule for the furniture items of various types. To do this, we must figure out how to multiply the matrices together. We know the HiringAnalysis, which is a matrix of (EmployeeCategory x Month), and we know the FurnitureAnalysis, which is a matrix of (EmployeeCategory x ItemType). The procurement schedule is a matrix of (ItemType x Month). So the matrix product we seek is
This is implemented in the formula
Finally, we compute cumulative procurement as the running sum of procurement.
Last Modified: Wednesday, 27-Apr-2016 04:15:26 EDT
For many of you, matrix multiplication and array arithmetic are new ideas. It’s easy to get lost in the details of how they work and then forget about why we use them.
To keep a clear view of the forest and avoid focusing only on the trees, remember why we use matrix multiplication and array arithmetic. Briefly, we use them because we find that it’s very often helpful to decompose a problem into parts (analysis), then do calculations on the parts, and finally reassemble the final solution from the results of those partial calculations (synthesis).
Matrix multiplication and array arithmetic provide us with very convenient methods for performing those intermediate calculations on the parts. They’re the tools that make analysis and synthesis so powerful.