Spreadsheet Models for Managers
Getting Access to Spreadsheet Models for Managers
If 
you use Excel to model businesses, business processes, or
business transactions, this course will change your life. You’ll learn how to create tools for yourself that will amaze
even you. Unrestricted use of this material is available in two ways.
- As a stand-alone Web site
- It resides on your computer, and you can use it anywhere. No need for Internet access.
- At this Web site
- If you have access to the Internet whenever you want to view this material, you can purchase on-line access. Unlimited usage. I’m constantly making improvements and you’ll get them as soon as they’re available.
To Order On Line
| Order "Spreadsheet Models for Managers, on-line edition, one month" by credit card, for USD 69.95 each, using our secure server, and receive download instructions by return email. |
| Order "Spreadsheet Models for Managers, on-line edition, three months" by credit card, for USD 199.00 each, using our secure server, and receive download instructions by return email. |
| Order "Spreadsheet Models for Managers, downloadable hyperbook edition" by credit card, for USD 199.00 each, using our secure server, and receive download instructions by return email. |
To Order by Mail
Make your check payable to Chaco Canyon Consulting, for the amount indicated:
|
And send it to: Chaco Canyon Consulting 700 Huron Avenue, Suite 19C Cambridge, MA 02138 |
To use the course software you’ll need some other applications, which you very probably already have. By placing your order, you’re confirming that you have the software you need, as described on this site.
Spreadsheet Models for Managers
This reading is especially relevant for Session 2Matrices and Matrix Multiplication
Outside of the context of business modeling, mathematicians have developed a set of techniques for handling arrays of numbers. It turns out that some of these techniques are very useful to us, especially when we’re using the techniques of analysis and synthesis to approach a modeling problem.
Using matrix multiplication, we can reduce dramatically the labor involved in modeling processes that deal with multiple categories of employees, customers, districts, products, or supplies. If you look for books about matrices, you’ll find a vast mathematical literature, and if you’re like most people, it can be a little intimidating. But Fear Not! The parts that we need are not that bad, even though they might look a little difficult at first. After you get used to these ideas, they’re very easy to use.
Here’s a quick summary of what you’ll find on this page.
- What is a matrix?
- Why is a matrix useful?
- The dimensions of a matrix
- How matrix multiplication works in Excel
- The transpose of a matrix
- Matrix products
- Matrix inverse
- Using matrix products
- What matrices to multiply
What is a matrix?
A matrix is a rectangular array of numbers. In Excel, or in any spreadsheet application program, we can represent a matrix as a range of cells with numerical entries. Actually, the elements of a matrix need not be numbers, but for our purposes, they always will be numbers.
Here’s an example of a matrix: 
Why are matrices useful?
Perhaps the best way to convey the usefulness of matrices
is by example. Suppose that you’re the manager of milk merchandising for a supermarket chain.
You can represent your inventory as a matrix of brand by size. In the matrix, each row contains
data for a particular brand of milk, and each column represents data for a given size. For
example, the data for quarts of Bessie brand might be in the first cell of the third row. The
half-gallon data might be in the second column of that same row. Analogous data for the Moo-Moo
brand might be in the fifth row. This is a concise, manageable representation.
The dimensions of a matrix
The dimensions of a matrix are given as a pair of integers, separated by an “x”. For example, the matrix above has dimensions 4x3. We say that it’s a 4x3 ("4 by 3") matrix. A matrix that has the same number of rows as columns is said to be “square.” The (3,2) element of a matrix is the number that’s in the second column of the third row.
The transpose of a matrix
The transpose of a matrix is a new matrix that’s obtained by interchanging the rows and columns of the original matrix. For example, the transpose of the matrix above is:
The Excel worksheet function that produces the transpose of a matrix is TRANSPOSE. The notation for the transpose of a matrix A is At.
Matrix products
We can define a kind of product of two matrices that turns out to be very useful in business modeling applications. It’s a little different from other kinds of products that you might know. It’s called the matrix product. Here’s how it works.
Let’s compute the product of two matrices, A·B. We’ll call the first factor of the product A and the second factor of the product B. To form the matrix product of two matrices, you compute the (i, j) element of the product as the result of summing the ordinary arithmetic product, element by element, of row i of the first factor and column j of the second factor. You must do this calculation for every element of the product matrix. The Excel worksheet function that implements matrix multiplication is MMULT.
For this product to be defined, the number of rows of the second factor must be equal to the number of columns of the first factor.
Here’s an example: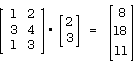 
Check this. Notice that the (1 1) element of the result, 8, is equal to 2*1+3*2.
Matrix inverses
The inverse of a matrix M is a matrix MI such that the matrix product M·MI (or MI·M) is an identity matrix. An identity matrix is a square matrix of zeros except for the diagonal, which consists solely of ones. Some matrices don’t have inverses. They are said to be singular. The left inverse of a matrix might not be the same as the right inverse, except when the matrix is square.
How matrix multiplication works in Excel
To make Excel compute the product of two matrices, A·B, follow these steps:
- Verify for yourself that A has as many columns as B has rows. If not, the product is not defined.
- Figure out the dimensions of the result. The result has as many rows as does the first factor, A, and as many columns as the second factor, B.
- Select a range of that shape. If A has 6 rows, and B has 3 columns, you would select a 6x3 range.
- Enter as an array formula =MMULT(A,B)
For examples of the use of matrices, see the demonstrations for Session 2.
Using matrix products
How on earth can such a complex
thing as a matrix product be useful in business modeling? Its usefulness comes about because it
so readily combines the pieces back together after you’ve decomposed a problem into parts. Let’s
go back to the milk department in the supermarket, and let’s compute the projected total value
of the inventory for Bessie Brand milk, week by week for 13 weeks. And let’s suppose that there
are three sizes of milk containers.
We first set up a price matrix. It has three rows, one for each size, and one column. So it’s a 3x1 matrix of size by dollars. Next, set up a projected inventory matrix. Again it has three rows, one for each size. It has 13 columns, one for each week, so it’s a 3x13 matrix of size by week.
The result we seek is a single row of 13 cells, indicating the total value of inventory for each week of the 13 weeks. It’s a 1x13 matrix of dollars by week.
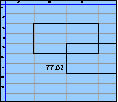
Concretely, let’s say that quarts cost $1.02, half gallons cost $1.78, and gallons $2.24.
Then the price matrix is P: 
.
And let’s suppose that the projected inventory Q is:
The result we seek is Pt · Q:
[245.86 236.14 249.26 243.82 255.28 235.28 246.94 244.84 242.74 254.30 267.04 239.04 256.90]
<snip>…
Some of the page you’ve been reading has been suppressed from this sampler. To see the complete version of this article, why not order the full course? It’s available at this Web site or in downloadable format.
| Order "Spreadsheet Models for Managers, on-line edition, three months" by credit card, for USD 199.00 each, using our secure server, and receive download instructions by return email. |
| Order "Spreadsheet Models for Managers, downloadable hyperbook edition" by credit card, for USD 199.00 each, using our secure server, and receive download instructions by return email. |
…<end snip>
Last Modified: Wednesday, 27-Apr-2016 04:15:26 EDT
For many of you, matrix multiplication and array arithmetic are new ideas. It’s easy to get lost in the details of how they work and then forget about why we use them.
To keep a clear view of the forest and avoid focusing only on the trees, remember why we use matrix multiplication and array arithmetic. Briefly, we use them because we find that it’s very often helpful to decompose a problem into parts (analysis), then do calculations on the parts, and finally reassemble the final solution from the results of those partial calculations (synthesis).
Matrix multiplication and array arithmetic provide us with very convenient methods for performing those intermediate calculations on the parts. They’re the tools that make analysis and synthesis so powerful.