Spreadsheet Models for Managers
Getting Access to Spreadsheet Models for Managers
If 
you use Excel to model businesses, business processes, or
business transactions, this course will change your life. You’ll learn how to create tools for yourself that will amaze
even you. Unrestricted use of this material is available in two ways.
- As a stand-alone Web site
- It resides on your computer, and you can use it anywhere. No need for Internet access.
- At this Web site
- If you have access to the Internet whenever you want to view this material, you can purchase on-line access. Unlimited usage. I’m constantly making improvements and you’ll get them as soon as they’re available.
To Order On Line
| Order "Spreadsheet Models for Managers, on-line edition, one month" by credit card, for USD 69.95 each, using our secure server, and receive download instructions by return email. |
| Order "Spreadsheet Models for Managers, on-line edition, three months" by credit card, for USD 199.00 each, using our secure server, and receive download instructions by return email. |
| Order "Spreadsheet Models for Managers, downloadable hyperbook edition" by credit card, for USD 199.00 each, using our secure server, and receive download instructions by return email. |
To Order by Mail
Make your check payable to Chaco Canyon Consulting, for the amount indicated:
|
And send it to: Chaco Canyon Consulting 700 Huron Avenue, Suite 19C Cambridge, MA 02138 |
To use the course software you’ll need some other applications, which you very probably already have. By placing your order, you’re confirming that you have the software you need, as described on this site.
Spreadsheet Models for Managers
Demonstrations for Session 8
Financial Models
We have one demonstration (2007+) for this session: Active Representations of Depreciation Schedules.
Active Representations of Depreciation Schedules (2007+)
[Sheet: DepreciationExample]
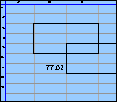
In this example, we compute the depreciation stream for a series of capital expenditures that are driven by a hiring stream. This hiring stream is held in the range named HireStream. Each time we hire a person, we must buy him or her a PC that costs $1.2 k, which is held in the cell named PCCost. The depreciation term is 4 years, or 16 quarters, and we’ll assume that we use a straight-line depreciation schedule. This parameter is held in the cell named DepreciationTerm. All parameters and input streams are shaded yellow, indicating that the user can adjust them.
We’ll compute both the cash expended per quarter and the depreciation cost per quarter required to support this hiring stream. And we’ll do it in a way that honors the Ripple Principle — if either of the parameters PCCost or DepreciationTerm, or if any part of the input stream HireStream is adjusted, the effects propagate correctly. It’s possible to obtain the same results without following this principle so rigorously, and in most cases that’s just fine. But we’ll illustrate here how you go about it so that if you need to, you can do it yourself.
The basic strategy is to compute the capital expenditure stream, then convolve that with the depreciation schedule to obtain the depreciation per quarter. The range CashExpenditure is the capital expenditure stream, obtained by multiplying PCCost by HireStream.
Perhaps the most difficult part of this example is the depreciation schedule itself, DepreciationPQ. We could have filled in the values for the depreciation as a simple formula:
in each of the first 16 cells of the range DepreciationPQ. But later, when someone adjusts DepreciationTerm, the number of cells that have that value would be wrong. For example, if someone sets DepreciationTerm to 12, we want only the first 12 cells to hold the value. So we must face the problem of not only figuring out what the value of one quarter’s depreciation is, but also which quarters should hold that value, and which should hold 0.
And there’s another problem, too. We’d like whatever formula we use to be transportable anywhere on the worksheet. That is, it shouldn’t assume that the depreciation stream always starts in, for example, Column C.
We accomplish all this using the IF and COLUMN worksheet functions. The formula is:
Here’s how it works. Let’s begin with the IF. It returns either 1 or 0, depending on the result of its first argument. If the first argument is TRUE, the IF returns 0, otherwise 1. So let’s now look at its first argument. To understand it, you must understand how column works. With no arguments, column returns just the column number of the cell that contains it in its formula. With a single argument, column returns the column number of the upper left cell of that argument, interpreted as a reference. So the first argument of the IF compares the column number of the cell that owns the formula with a formula that involves the column number of the first cell of DepreciationPQ. If the cell in question has a column number that’s more than DepreciationTerm-1 greater than the column number of DepreciationPQ, then the IF returns 0, otherwise 1. This is just what we want. We take this 0 or 1 and multiply by 1/DepreciationTerm.
Since the formula we’ve installed contains nothing but constants, user-defined names, and worksheet functions, it’s eligible to be the definition of a user-defined name. (It could also contain explicit cell or range references, and still be eligible.) For instance, we could define the name DepPQ to be the above formula, and then use that name as the entire formula of each cell, instead of the formula we did use. This technique doesn’t gain us much in this example, but if we were developing a larger model in which we used the above formula in several places, possibly in several worksheets, it might save us some trouble. For instance, suppose we had installed a particular depreciation method in a model, and then received word that the CFO had decided to use a different depreciation method. All we would have to do then is update the definition of DepPQ. We wouldn’t have to chase around the workbook editing all the cells that contain the formula that has to change. Or suppose we develop a model for one customer or client, and then later, we want to re-use that model, modified, for another customer or client who uses a different depreciation schedule. All we would have to do then is update the definition of DepPQ.
OK, so now we have a Ripple-proof depreciation schedule. The rest of this example is pretty simple. To get the depreciation stream, Convolve that depreciation schedule with the capital expenditure stream, as is done in the range Depreciation.
Total assets are just cash outlays minus depreciation, and cumulative cash is just a running sum of cash outlays.
This example could have been done more simply if we had violated the Ripple Principle. But then, if we found that the Depreciation Term changed, or if we tried to apply this worksheet in a different model with a different depreciation term, we might forget to adjust the depreciation schedule, or we might do it incorrectly. Following the Ripple Principle is the safest, lowest-cost course in most cases.
By the way, it could be even messier. Suppose that the depreciation term were not an integer number of time periods. That would be most unusual, but it’s possible. In that case, the last cell of the non-zero part of the depreciation schedule would have a different value — some fraction of the full cell value. Another possibility is a non-uniform depreciation — different values for different cells. If you can figure out a formula for the schedule, that’s best. But it might be very difficult to do. You might just have to fill in the numbers.
It’s also possible to use depreciation schedules other than straight-line depreciation, which is what we did above. The last row, labeled SOYDDepreciationPQ, implements the Sum-of-the-Years digits method of depreciation. In SOYD depreciation, if the useful life is N periods, the amount depreciated in period k, if salvage value is zero, is given by:
Such a depreciation schedule writes off more of the asset in the early periods, as compared to straight-line depreciation. The formula that implements this in Excel is:
We could then carry this depreciation schedule forward just as before. Of course, it’s much easier to use the built-in worksheet function syd.
Finally, note that, as usual, we’ve formatted with double-line borders the first two cells of the rows for Total Assets and Cumulative Cash, to indicate that the formulas for those cells differ from the formulas for the remaining cells of their respective rows. This indicates to future maintainers that filling their formulas across their respective rows will introduce errors.
Last Modified: Wednesday, 27-Apr-2016 04:15:26 EDT
In the demonstration for this session, we installed a formula for depreciation that looked pretty complicated. It does save maintenance trouble, though, when the depreciation term changes for any reason. But what happens when the depreciation schedule changes in a more radical way? What if the depreciation schedule is made to be some form other than linear?
The end of this session’s demonstration gives an example of an alternative schedule, but as you can see, its formula is very different. If we’re developing a complex model with several applications of depreciation formulas, and the depreciation formulas must be changed, we would have a significant maintenance task on our hands. To avoid that kind of labor, we can define a user-defined name that contains the depreciation formula. For more about this technique, see the tip box in the narrative for this session’s demonstration.