
Spreadsheet Models for Managers
Getting Access to Spreadsheet Models for Managers
If  you use Excel to model businesses, business processes, or
business transactions, this course will change your life. You’ll learn how to create tools for yourself that will amaze
even you. Unrestricted use of this material is available in two ways.
you use Excel to model businesses, business processes, or
business transactions, this course will change your life. You’ll learn how to create tools for yourself that will amaze
even you. Unrestricted use of this material is available in two ways.
- As a stand-alone Web site
- It resides on your computer, and you can use it anywhere. No need for Internet access.
- At this Web site
- If you have access to the Internet whenever you want to view this material, you can purchase on-line access. Unlimited usage. I’m constantly making improvements and you’ll get them as soon as they’re available.
To Order On Line
| Order "Spreadsheet Models for Managers, on-line edition, one month" by credit card, for USD 69.95 each, using our secure server, and receive download instructions by return email. |
| Order "Spreadsheet Models for Managers, on-line edition, three months" by credit card, for USD 199.00 each, using our secure server, and receive download instructions by return email. |
| Order "Spreadsheet Models for Managers, downloadable hyperbook edition" by credit card, for USD 199.00 each, using our secure server, and receive download instructions by return email. |
To Order by Mail
Make your check payable to Chaco Canyon Consulting, for the amount indicated:
|
And send it to: Chaco Canyon Consulting 700 Huron Avenue, Suite 19C Cambridge, MA 02138 |
To use the course software you’ll need some other applications, which you very probably already have. By placing your order, you’re confirming that you have the software you need, as described on this site.
Spreadsheet Models for Managers
Problem Set 2Session Links
Analysis and Synthesis
Be sure to check the list of worksheet functions that are needed for the homework assignments, to see which new functions (if any) might help with this assignment.
For a quick way to copy homework problem data into your homework solution, see “Avoid retyping homework problem data.”
Since macros aren’t permitted in this homework assignment, be certain that the workbook you submit for grading has no macros. Read about how to check your workbooks for macros.
Remember that some problems are slight extensions of what we show you in class, in the demonstrations and in the session notes, and some problems are somewhat ambiguous. This is intended to parallel what you’ll frequently encounter at work. If you feel a bit confused, there are some things you can do to help clarify things.
Before attempting this homework, you might find it helpful to read about:
Numbers in square brackets to the right of the problem numbers indicate point values.
Create a worksheet that you use to compute the following matrix products. Store each matrix factor and each product in its own portion of the worksheet.
Find the matrix product of A•B where A = 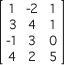 and B =
and B = ![]() . Your result should be a single 4x2 range.
. Your result should be a single 4x2 range.
Can you find the matrix product B•A of the matrices in (a)? If you can, do it, and “AnswerB” should be a local name defined to be a range of appropriate size. If not, type your explanation of why not directly into the worksheet in a cell, and Your result should be a single cell.
Find the matrix product C•D where C = ![]() and D =
and D = ![]() .
Your result should be a single 3x3 range.
.
Your result should be a single 3x3 range.
Verify that (C•D)t = Dt • Ct using the matrices C and D of part (c). Express this verification by computing the cell-by-cell difference of the respective matrix elements, and showing that the difference is a matrix of zeros. Your result should be a single 3x3 range.
In parts (e), (f) and (g) of this problem, we explore a different
way to express matrix multiplication. Define a named array MatrixE that contains
![]() and a named array MatrixF that contains
and a named array MatrixF that contains ![]() . Define the names
Array11 to be the first column of MatrixE, Array12 to be
the second column of MatrixE, Array21 to be the first row of
MatrixF, and Array22 to be the second row of MatrixF.
Find the array product of Array11 and Array21. Also find the array
product of Array12 and Array22. By subtracting the matrix product
Array11 • Array21 from the array product of Array11
and Array21, verify that the array product of Array11 and
Array21 is equal to the matrix product Array11 •
Array21. Your result should be a single 2x2 range.
. Define the names
Array11 to be the first column of MatrixE, Array12 to be
the second column of MatrixE, Array21 to be the first row of
MatrixF, and Array22 to be the second row of MatrixF.
Find the array product of Array11 and Array21. Also find the array
product of Array12 and Array22. By subtracting the matrix product
Array11 • Array21 from the array product of Array11
and Array21, verify that the array product of Array11 and
Array21 is equal to the matrix product Array11 •
Array21. Your result should be a single 2x2 range.
Find the sum of the two array products you found in (e). Your result should be a single 2x2 range.
Verify that the result in (f) is identical to the matrix product MatrixE • MatrixF. Express this verification by computing the cell-by-cell difference of the respective matrix elements, and showing that it’s a matrix of zeros. Your result should be a single 2x2 range.
Top management  of Geodesic
Telecommunications, Inc., has asked you to take a closer look at its launching plan (see
Problem 1.1). Recall that they plan to build a global satellite network to provide
wireless communications service to the world. To accomplish this, they plan to launch 240
communications satellites into low earth orbit.
of Geodesic
Telecommunications, Inc., has asked you to take a closer look at its launching plan (see
Problem 1.1). Recall that they plan to build a global satellite network to provide
wireless communications service to the world. To accomplish this, they plan to launch 240
communications satellites into low earth orbit.
In this problem, you’ll examine costs from a perspective that differs from Problem 1.1. As in Problem 1.1, satellites are launched in groups of 8 by a single rocket, but not all satellites on a given rocket are identical. Some of the satellites are of a type called “Master Router” which handles communications between the satellites in the group, and some are “Soldier” satellites that carry the routine earth-orbit communications for customers. The Master Router also handles earth-orbit communications, but it sometimes happens that a customer on the ground who is connected to one satellite wants to communicate with another customer on the ground, who is connected to a different satellite. In this case, the two satellites contact the Master Router, which provides directions to them on how to route the communication.
There are six basic components needed to build all of the satellites. The components required to build the satellites are shown in the table below.
| Component | Function | Master Router |
Soldier | Cost (k$) |
| Relay Communicator |
Transmit and receive between Soldiers and Master Router |
6 | 1 | 142 |
| Spare Relay Communicator |
Spare above | 2 | 1 | 149 |
| Earth/Orbit Communicator |
Transmit and receive between earth and a satellite |
1 | 1 | 177 |
| Relay Antennas | Antennas for communications between Soldiers and Master Router |
5 | 1 | 80 |
| Scheduling Equipment |
Schedule conversations with Master Router |
1 | 0 | 105 |
| Base Unit | Chassis, power supply, attitude control, etc. |
1 | 1 | 485 |
Starting with the fourth launch, three Master Router satellites are launched as part of the payload of every fourth rocket. The other five satellites on those rockets are Soldiers. All other satellites on all other rockets are Soldiers. Launches occur at the rate of three per month. Specifically, the first three launches are all Soldiers. The fourth launch is comprised of three Master Routers and five Soldiers. Thereafter, the same pattern of four launches repeats.
Compute the cumulative numbers of Master Routers and Soldiers in orbit at the end of each of the first 10 months. Display your result with Master Routers in the top row, and Soldiers in the bottom row. Your result should be a single 2x10 range.
Compute the cumulative numbers of each of the six components required each month for the first 10 months. Your answer should be in the form of six rows of 10 numbers, one row for each of the six components. Your result should be a single 6x10 range.
Using the result of (b), compute the cumulative cost, in millions of dollars, of acquiring the six categories of components, by component category, by month. Also compute a monthly total. If you could not complete (a), create a row of 10 numbers, having the values 1 to 10, and use that instead. Your answer should be in the form of seven rows of 10 numbers, one row for each of the six components, and a seventh row at the bottom for the total. Your result should be a single 7x10 range.
Compute the cumulative monthly total in (c) directly, using a single array formula without computing the intermediate numbers of components you need. Your result should be a single 1x10 range.
El Capitan Insurance is planning to roll out a new series of annuities this
winter. The products are somewhat technical, and there are five of them. The Wholesaler Support
Group, which has five staff, is expected to contact each of El Capitan’s 50  wholesalers by telephone during the week of the product introduction
to explain the new products to them, and to guide them in choosing target markets.
wholesalers by telephone during the week of the product introduction
to explain the new products to them, and to guide them in choosing target markets.
Two of the Wholesaler Support Group staff, Vincent and Victoria, are experienced veterans. Because they have established personal relationships with the wholesalers, they’re more effective and productive than the three rookies on the staff, Rose, Richard, and Rachel. Each staffer has 10 wholesaler accounts, but not all wholesalers will sell all products equally. The expected number of hours required by each staffer to brief a wholesaler on each of the five products is as shown in Table 2.3.1.
Note: This problem is designed to give you an idea of how it feels when you spend a lot of time working something out, and then your customer says something like “Remember I told you we had 6 products? Well, we’re canceling Number 2. Have a nice day.” This is typical. Normally, the rework is major, expensive and, because it’s often done in a hurry, it’s just as often wrong. We’re trying to show you in this problem how to anticipate the need for flexibility when you build models. That way, you can avoid getting caught in the position of having to make complex major changes close to the deadline because somebody else changed something.
The hours of operation of El Capitan Insurance are 8 AM to 5 PM Monday through Friday. Everyone on the staff takes an hour for lunch starting at Noon. If all staffers start contacting their wholesalers at 8 AM Monday morning, and work eight-hour days, and if they talk to each wholesaler about each product, when will they each finish? State your answers as a day of the week and a time of day for Veterans and for Rookies. If the day is a day of the following week, use the word “Following.” For example, if the day is the following Wednesday, enter “Following Wednesday” for the day. Your result should be a single 2x1 range.
Note: Don’t get involved with using Excel’s date and time functions, unless you already know how they work. Just compute the hours required for Vets and for Rookies, and then convert that to a day and time using whatever means you can, including pencil and paper. Enter each day and time as text into a cell of the worksheet, one for Vets and one for Rookies.
The expected unit sales of Victoria’s ten wholesalers for each of the five products are as shown in Table 2.3.2. Assume also (though this is a bit unrealistic) that Rose’s ten wholesalers are expected to perform identically.
Table 2.3.2: Expected Unit Sales of new products by Victoria’s 10 wholesalers
| Wholesaler | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Product A | 397 | 503 | 914 | 680 | 62 | 268 | 810 | 528 | 801 | 278 | |
| Product B | 141 | 923 | 170 | 603 | 18 | 45 | 217 | 796 | 744 | 951 | |
| Product C | 754 | 571 | 273 | 164 | 69 | 839 | 372 | 557 | 128 | 679 | |
| Product D | 515 | 978 | 354 | 561 | 379 | 355 | 196 | 77 | 310 | 407 | |
| Product E | 139 | 67 | 906 | 615 | 648 | 951 | 15 | 522 | 635 | 591 |
- Note: Before you start this one, read part (d), especially the note.
- The reason for posing these two parts in this way is to emphasize that in real life, we often are asked to make “just a small change” to some work we’ve already done. Although the change might be small, the amount of work required to implement it can be just as great as the work we have done so far (or greater!). If you work in that kind of environment (and most of us do), it helps to set things up so they can be easily changed.
As the manager of the Wholesaler Support Group of El Cap, you decide that it’s best for each of your people to be selective in briefing the wholesalers. If Rose and Victoria brief only those expected to sell more than 550 units of a product, and if they brief their wholesalers on only those products, how long will it take each of them to brief each wholesaler (in hours)? Express your result as a 2x10 range, with the top row representing the hours Victoria spends with each of the 10 wholesalers, and the bottom row representing the hours Rose spends with each of the 10 wholesalers. Your result should be a single 2x10 range.
Repeat part (b) for a threshold of 650 units. Your result should be a single 2x10 range.
Marketing is considering dropping Product E. Repeat Part (b) without Product E. Your result should be a single 2x10 range.
Note: if you were clever in setting up your answer to (b), this one isn’t much work.
Last Modified: Sunday, 03-Aug-2025 03:54:37 EDT
For many of you, matrix multiplication and array arithmetic are new ideas. It’s easy to get lost in the details of how they work and then forget about why we use them.
To keep a clear view of the forest and avoid focusing only on the trees, remember why we use matrix multiplication and array arithmetic. Briefly, we use them because we find that it’s very often helpful to decompose a problem into parts (analysis), then do calculations on the parts, and finally reassemble the final solution from the results of those partial calculations (synthesis).
Matrix multiplication and array arithmetic provide us with very convenient methods for performing those intermediate calculations on the parts. They’re the tools that make analysis and synthesis so powerful.