well-understood task
is relatively narrow.
by Rick Brenner
Have you ever worked on a complex technology project that was completed on time? Probably not. And when a project is late, we usually feel bad about it, and the people who depend on us feel let down. The problem is that our intuition about scheduling is misleading us. It's all so avoidable — if only we understand what's really going on, we can dramatically improve our ability to project schedules.
On May 29, 1998, Intel announced that it had delayed production of its Merced chip by more than six months. A few days later, an article in The Wall Street Journal for June 1, 1998, reported that Intel attributed the delay to having "underestimated the task of testing the complex chip."
And lest we believe that this situation is much improved since then, The Wall Street Journal for August 30, 2004, reported that the then-next version of Windows, code-named Longhorn (which eventually became Vista), would ship "without one of its most high-profile features, further delaying a software advance that Chairman Bill Gates has tried to make a top priority at the company for more than a decade." Vista, which was originally scheduled for late 2003, finally shipped in January, 2007. The beat goes on.
We've all been there — the original time, duration, and effort estimates or guesses for each of the dozens (or hundreds!) of interlocked tasks of a complex project all seemed reasonable. Most of them actually came in pretty close to what was anticipated, or at least, not too far off. But the project as a whole, for some reason, defied our ability to project its delivery date. In the wrong direction. By a lot.
This has happened so consistently that maybe Marketing and Sales no longer believe Engineering, Development, or IT when it comes to schedule. It happens in so many industries, with people using so many different technologies, that one begins to wonder if there isn't something fundamental going on.
What we're seeing is an effect that's observable in all systems whose behaviors are best described by statistical distributions. The cause of the lateness is traceable to the shapes of those distributions.
In brief, the problem is that we tend to use as a guess or estimate of task duration the most likely value, instead of the average value, or something larger than the average. That wouldn't be a problem in itself, but for most technology projects, the most likely value of a task's duration is much less than the average value. Combine that with the fact that most complex projects consist of many such tasks in sequence, and it's not hard to see how we get into trouble.
That's it. The rest of this essay explains all this in a more detailed way:
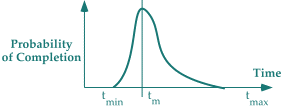
Tasks in projects are usually so complex that if we were to repeat them under identical conditions, the time required to complete them would vary. After all, people are involved in performing these tasks, and as you may know, the behavior of people is non-deterministic. So when we estimate or guess the duration of a task, we're really dealing with a range of possible outcomes. If plotted as a distribution, the actual results for a number of identical trials would have a shape such as shown in the figure below. There's a minimum duration, a most likely duration, and a maximum duration.
The shape of this distribution varies with the nature of the task. For example, if we've done the task many times, and everything involved in it is fairly predictable, the minimum and maximum duration are close together. The distribution is probably very narrow. If the task has never been tried before, and some aspects of the execution are poorly understood, the minimum duration and maximum duration might be more widely separated — our performance on the task could be quite variable. For example, pouring the concrete for a driveway is a task that's well understood. If you measure the time required by experienced professionals to pour a specific kind of driveway, you would probably arrive at a fairly narrow distribution. On the other hand, building a Space Shuttle is a less well-understood activity. The distribution of durations for that activity is more likely to be fairly broad.
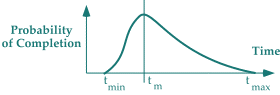
Distributions for the duration of less predictable activities have another significant feature. Although the minimum duration is probably well below the most likely duration, the spacing between them is usually far less than the spacing between the most likely duration and the maximum duration. The distributions are likely to have shapes like the ones below.
This comes about very naturally. While there are some pretty hard limits on how quickly things can happen, there are no analogous limits on how slowly things can happen. For example, no matter how hard you try, you probably cannot get to the conference room in the other building in less than 45 seconds — even if you run. But even without trying, it can sometimes take you 20 minutes, even though it's only a five-minute walk, depending upon whom you run into on the way over. So if you're prudent, you leave a little extra time to get there for the meeting, and even then, you're sometimes late.
This is just a small example. Now imagine the distribution of times required to execute a complex system test. If all goes well, it might take three days — never less. But if things don't go well — it could take weeks.

Technology projects are usually poorly understood — they've never been done before. That's why they're interesting in the first place. That is, the organizations that mount technology projects hope to achieve some significant result never before achieved.
This quality of being the first of its kind is one of the defining characteristics of a technology project. When we decide to replace an antiquated elevated freeway with tunnels, we're executing a technology project. When we develop a new piece of software because we think it will provide some functionality that we cannot obtain in the open market, we're executing a technology project. And the probability distributions of durations of projects that are less well understood are broad.
Whatever the shape, let's suppose we always know the most likely value of the duration of a task. This is a dubious assumption, but it clearly represents the best case — if we knew this number, we expect to do well at estimating schedules. And let's say that we use the most likely value of the duration distribution as the anticipated duration for each task. From this we can show that most projects would be very late indeed.
For purposes of this illustration, assume that all tasks are statistically independent. This means that the probability of completing any task in any given time is unaffected by what happened with the others. In real projects, tasks can interact in many ways, so this simplifying assumption is only approximately correct. It has some validity, because usually the things that cause bad news on a given task (aside from propagation delays) are unique to that task. The assumption of statistical independence has a most noble lineage — it's one of the basic axioms of the PERT method. Without this assumption, it's difficult to make any predictions at all about project schedules.
Another assumption we need is that the system we're modeling is time-invariant. That is, we assume that the properties of the tasks of a project that we model with these duration distributions do not change. This assumption is also somewhat unjustified, because we do know that people learn — they get better at what they're doing as time goes on. Or at least we hope so. But for purposes of project scheduling, we assume that things remain fairly constant.
Now consider a project consisting of two tasks, performed serially, with identical duration distributions. And let's say that we use the mean (also called "average") duration of each task as the estimate for the duration of each task. What is the probability that the duration of the project is less than or equal to the sum of the estimates for the two tasks?
All we have to do is to figure out all the ways we could possibly come in early or on time, compute the probability of each of those, and add them up. Well, without knowing the details of the two distributions, that's impossible. But if we did know the distributions, we know how we would do it.
We can say some things right away. For example, if each of the tasks finishes in a time less than or equal to what we estimated, the project certainly will. The probability of the first task doing so is 50%, and the same for the second. So the probability of both of them doing so is 50% of 50%, or 25%. So right away, we know that the probability of the project finishing at or below estimate is at least 25%. It's actually better than that, though.
The reason it's better is that we can be late on one of the tasks if the other is early enough. If the two deviations from the estimate compensate for each other by canceling out (or better yet, if we're earlier on one than we are late on the other) then the project comes in on schedule (or better). So we pick up another chunk of probability from these compensation situations. It turns out, in fact, that if the probability distributions of the durations of the tasks are symmetric about their average values, then the size of this component is also 25%. In that case, the chance of the project coming in at or below estimate is 50%.
This compensation phenomenon is critical to understanding why projects are usually late.
So far, this simple example seems consistent with our intuition. We have a 50% shot at coming in on time for each task, and a 50% shot for the project. Now it gets tricky. Look at all the assumptions we made:
When we make these assumptions, we find that our intuition is confirmed: the probability that the project completes on schedule (or better) is in line with our expectations. But this example is pretty far from real life.
Let's now relax some of these assumptions, so as to conform better to real life, and see what happens to the results.
If we increase the number of tasks in the serial chain, but leave everything else as is, it turns out that the result is the same — it conforms to our intuition. So that assumption isn't a problem. It simply serves as a simplification that we can use to explore the other issues.
Statistical independence, the second assumption, is discussed above. While it isn't strictly valid, it's good enough for any purposes of project management.
Requiring the duration distributions of all tasks to be identical isn't very realistic. In a real project, tasks take different lengths of time, and the distribution shapes can vary. Back in the days when PERT was very popular, people got fairly good results by assuming that all task durations obeyed a Beta distribution, which is the assumption of the PERT model. PERT did allow each task to have its own unique Beta distribution, determined by estimation, so that gave the model the flexibility it needed to model duration distributions of different widths and shapes. This assumption is one we ought to look at more closely.
Requiring that the estimated duration be equal to the mean duration is also unrealistic. Most estimates are devised so that the estimate coincides with the most likely duration. We'll also consider the effects of this assumption.
Finally, the assumption that the duration distribution is symmetric about the mean is also unrealistic, and we'll examine that as well.
We can address all three of these issues by building on all the work that was done to develop the PERT technique. In fact, if we use a Beta distribution for the duration of each task, we know from experience that the results are fairly realistic, and we've addressed all three of the open issues. So why are projects always late?
The answer is that the estimates most of us make for the duration of a task are of the "most likely" type. That is, we tend to use as an estimated duration the most likely value of the duration. And since the most likely value of the duration is usually less than the mean duration, for most distributions in real life, we tend to bias our estimates towards the short end of the distribution, as illustrated below.

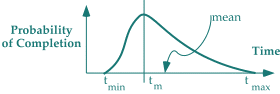
For a single task, this isn't good, but it isn't a catastrophe. True, on the average, our performance would be less than stellar. Depending upon the exact shape of the distribution, we would find that typically, we would be underestimating the actual duration by about 10-20%. But the problem becomes much more severe when we look at projects in which the project duration is the result of several such underestimates, in series, as would be the case along the critical path of a complex technology project.
The problem becomes more severe in complex technology projects because of the compensation phenomenon discussed above. In a two-task, serial project in which the distributions are reasonably realistic in shape, the probability that a task completes before the most likely duration is less than 50% — it might be 35% or even less than that. And if the minimum duration is close to the most likely duration, as shown above, the distribution has a long tail at the long-duration end, containing a significant amount of probability, that can't be canceled out by short durations in other tasks. In this case, the compensation phenomenon has only minor effects, and the result is that if we're significantly late on some tasks, no amount of early delivery on other tasks can compensate for it.
The conventional way to deal with this problem is to use as estimates or guesses the most likely values of the duration distributions of each task, padded by some amount. Since the amount of the pad is usually chosen by intuition, we really have no idea where, on the duration distribution, the estimate of a given task lies — indeed, even with a pad, we might still be below the mean of the distribution, especially for a task that's relatively less well-understood. Such tasks have duration distributions with very long tails, which drive the mean duration out very far.
If G is the gap between the mean of the distribution of the duration of a task and the estimate or guess you use for that task (which is often the most likely duration for that task), then you can expect that the project will be "late" by an amount equal to the sum of the Gs for the duration distributions of each task in the critical path. That is, after all, the meaning of "expected value."
All it takes is a few of those long-tailed distributions in the critical path to dramatically lower the accuracy of your project estimates. To minimize their effects, choose estimates that lie far out on the tails of their duration distributions. If you choose your estimates for the high-risk tasks far enough out, then those tasks won't be able to wreck your schedule except in the very remote event that they come in later than your estimate. For other tasks, those that are better understood and therefore lower risk, you can use the mean of the duration distribution for your duration estimate. You can view this conservative approach to estimation as part of your risk mitigation program.
Even tasks with long-tailed distributions that are not on the critical path can cause trouble. How? By getting into the critical path, which is very easy for them to do. Here are a couple of simple things that can cause this:
So it's probably a good idea to estimate all tasks with long-tailed duration distributions conservatively.
If you follow these guidelines, the chances that your project will be completed on schedule
will much more closely fit with the expectations of your sponsors. ![]() Top
Top
Is your organization as good as it can be at scheduling complex technology projects? Through consulting, workshops, or coaching, I can help your people learn to create complex project schedules that stick.
Are you a writer, editor or publisher on deadline? Are you looking for an article that will get people talking and get compliments flying your way? You can have 500-1000 words in your inbox in one hour. License any article from this Web site. More info
Send an email message to a friend
rbrenjTnUayrCbSnnEcYfner@ChacdcYpBKAaMJgMalFXoCanyon.comSend a message to Rick
![]() A Tip A Day feed
A Tip A Day feed
![]() Point Lookout weekly feed
Point Lookout weekly feed
 My blog, Technical Debt for Policymakers, offers
resources, insights, and conversations of interest to policymakers who are concerned with managing
technical debt within their organizations. Get the millstone of technical debt off the neck of your
organization!
My blog, Technical Debt for Policymakers, offers
resources, insights, and conversations of interest to policymakers who are concerned with managing
technical debt within their organizations. Get the millstone of technical debt off the neck of your
organization!